The Data Driven Newsvendor

The newsvendor problem is the classical single period inventory problem that refers to a situation in which a seller (the newsvendor) has to determine the order quantity of perishable goods for the next selling period under uncertainty in demand. The traditional way to solve the problem assumes that the demand distribution is known. In practice, however, we almost never know the true demand distribution.

In the following tutorial, you will get to know different approaches to solve the newsvendor problem when the underlying demand distribution is unknown but the decision maker has access to past demand observations. In this context, we consider the decision problem of Yaz, a fast-casual restaurant in Stuttgart. In addition, you will learn how to apply these approaches using our Python library ddop.

The tutorial is structured in 4 main parts:

• In Part 1, we first introduce the newsvendor problem by considering the real-world example of Yaz

• In Part 2, we explore and pre-process the Yaz-Dataset

• In Part 3, we discuss and implement the traditional parametric approach to solve the newsvendor problem

• In Part 4, we present different data-driven approaches to solve the newsvendor problem. Moreover, we show how to use ddop to apply them on the Yaz data.

Getting started

Before jumping into the tutorial, you should know the basics of Python and be familiar with well known libraries like numpy, pandas, and scikit-learn. To execute code, make sure you have an empty Python virtual environment installed on your computer. Alternatively, you can run through the tutorial via our Jupyter notebook on Google Colab. Once you are ready to start, you can install and load the libraries that we are going to need in the following:

pip install ddop==0.7.5 seaborn==0.11.0 matplotlib

from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd

Part 1: The Newsvendor Problem at Yaz

Let us now start by introducing the decision problem at Yaz. Yaz is a fast casual restaurant in Stuttgart providing great oriental cuisine. The main ingredients for the meals, such as steak, lamb, fish, etc., are prepared at a central factory and are deep-frozen to achieve longer shelf lives. Depending on the estimated demand for the next day, the restaurant manager has to decide how much of the ingredients to defrost over night. These defrosted ingredients/meals then have to be sold within the following day. If the defrosted quantity was too low, each unit of demand that cannot be satisfied incurs underage cost of \(cu\). On the other hand, if the quantity was too high, unsold ingredients must be disposed of at overage cost of \(co\). Therefore, the store manager wants to choose the order quantity that minimizes the sum of the expected costs.

More formally, the problem that the store manager is trying to solve is given by:

\begin{equation} \min_{q\geq 0} = E_D[cu(D-q)^+ + co(q-D)^+], \tag{1} \end{equation}

where \(D\) is the uncertain demand, \(q\) is the order quantity, \(cu\) and \(co\) are the per-unit under and overage costs, and \((\cdot)^+ := \max\{0,\cdot\}\) is a function that returns 0 if its argument is negative, and else its argument. The optimization problem at hand is what is known as the newsvendor problem. If the demand distribution is known, then the optimal decision can be calculated as follows:

\begin{equation} q^*=F^{-1}\biggl(\frac{cu}{cu+co}\biggl)=F^{-1}(\alpha), \tag{2} \end{equation}

where \(F^{-1}(\cdot)\) is the inverse cumulative density function (cdf) of the demand distribution, and \(\alpha\) is the service level. Unfortunately, the store manager can not directly solve equation (2) since he does not know the true distribution of \(D\). However, he has collected past demand data that he can use for decision making.

Part 2: The Yaz Dataset

The data collected by the restaurant manager includes the demand for the main ingriedients at Yaz over a number of days. In addition it provides different features that the manager expected to be predictive for demand. In the following, we will use this dataset to solve the newsvendor problem when the underlying demand distribution is unknown. The dataset can be accessed from the ddop.datasets module using the load_yaz method:

from ddop.datasets import load_yaz
yaz = load_yaz()

load_yaz returns a dictionary-like object containing the following attributes:

• data: the feature matrix

• target: the target variables

• DESCR: the full description of the dataset.

To get more details about the dataset, let us first print the description.

print(yaz.DESCR)

.. _yaz_dataset:

YAZ dataset
----------------

This is a real world dataset from Yaz. Yaz is a fast casual restaurant in Stuttgart providing good service
and food at short waiting times. The dataset contains the demand for the main ingredients at YAZ.
Moreover, it stores a number of demand features. These features include information about the day, month, year,
lag demand, weather conditions and more. A full description of targets and features is given below.


**Dataset Characteristics:**

    :Number of Instances: 765

    :Number of Targets: 7

    :Number of Features: 12

    :Target Information:
        - 'calamari' the demand for calamari
        - 'fish' the demand for fish
        - 'shrimp' the demand for shrimps
        - 'chicken' the demand for chicken
        - 'koefte' the demand for koefte
        - 'lamb' the demand for lamb
        - 'steak' the demand for steak

    :Feature Information:
        - 'date' the date,
        - 'weekday' the day of the week,
        - 'month' the month of the year,
        - 'year' the year,
        - 'is_holiday' whether or not it is a national holiday,
        - 'is_closed' whether or not the restaurant is closed,
        - 'weekend' whether or not it is weekend,
        - 'wind' the wind force,
        - 'clouds' the cloudiness degree,
        - 'rain' the amount of rain,
        - 'sunshine' the sunshine hours,
        - 'temperature' the outdoor temperature

    Note: By default the date feature is not included when loading the data. You can include it
    by setting the parameter `include_date` to `True`.

As we can see, the dataset includes the demand for seven main ingredients over 765 days. In addition it provides 12 demand features including calendar information as well as weather conditions. To take a look at the feature matrix, we can us the data attribut.

yaz.data

	weekday	month	year	is_holiday	is_closed	weekend	wind	clouds	rain	sunshine	temperature
0	FRI	OCT	2013	0	0	0	1.9	7.7	0.1	150	15.9
1	SAT	OCT	2013	0	0	1	2.7	6.9	10.7	0	13.2
2	SUN	OCT	2013	0	0	1	1.4	8.0	0.4	0	10.6
3	MON	OCT	2013	0	0	0	2.3	6.4	0.0	176	13.3
4	TUE	OCT	2013	0	0	0	1.7	8.0	0.0	0	13.5
...	...	...	...	...	...	...	...	...	...	...	...
760	TUE	NOV	2015	0	0	0	1.6	8.0	0.0	0	3.5
761	WED	NOV	2015	0	0	0	1.8	2.2	0.0	362	14.6
762	THU	NOV	2015	0	0	0	1.8	0.7	0.0	405	14.7
763	FRI	NOV	2015	0	0	0	1.9	6.9	0.0	44	16.0
764	SAT	NOV	2015	0	0	1	1.9	5.6	0.0	46	17.3

765 rows × 11 columns

Analogously, we can access the demand data by using the target attribute.

yaz.target

	calamari	fish	shrimp	chicken	koefte	lamb	steak
0	6	6	12	40	23	50	36
1	8	8	5	44	36	37	30
2	6	5	11	19	12	22	16
3	4	4	2	28	13	28	22
4	7	4	9	22	18	29	29
...	...	...	...	...	...	...	...
760	2	0	8	47	30	32	32
761	2	1	13	38	31	14	38
762	1	8	11	47	32	42	24
763	3	6	9	50	40	44	32
764	0	2	2	45	25	6	20

765 rows × 7 columns

Note that in the following analysis we want to focus on only a single product, steak. Consequently, we select only the demand column for steak and save it to the target variable y. In addition, we assign the feature matrix to variable X and create a data frame df that contains both feature and target data.

y = yaz.target['steak']
X = yaz.data
df = pd.concat([X,y], axis=1)

Exploratory Data Analysis (EDA)

So far we have seen a short snippet of the Yaz dataset, as well as a textual description which is important for a basic understanding. In the following, we will now explore the data in more detail to find insights that will hopefully help us make good decisions later on. As first step, we compute various descriptive statistics of our dataset (including the mean, standard deviation, minimum, and maximum) using the describe method from pandas.

df.describe()

	is_holiday	is_closed	weekend	wind	clouds	rain	sunshine	temperature	steak
count	765.000000	765.000000	765.000000	765.000000	765.000000	765.000000	765.000000	765.000000	765.000000
mean	0.032680	0.006536	0.288889	3.061438	5.072941	0.818824	235.406536	13.291634	22.333333
std	0.177913	0.080633	0.453543	1.237139	2.361906	2.694543	207.111854	7.656709	10.082643
min	0.000000	0.000000	0.000000	1.100000	0.000000	0.000000	0.000000	-5.900000	0.000000
25%	0.000000	0.000000	0.000000	2.200000	3.100000	0.000000	34.000000	7.000000	16.000000
50%	0.000000	0.000000	0.000000	2.900000	5.600000	0.000000	205.000000	13.600000	21.000000
75%	0.000000	0.000000	1.000000	3.600000	7.200000	0.200000	405.000000	18.300000	27.000000
max	1.000000	1.000000	1.000000	11.400000	8.000000	37.400000	782.000000	34.900000	82.000000

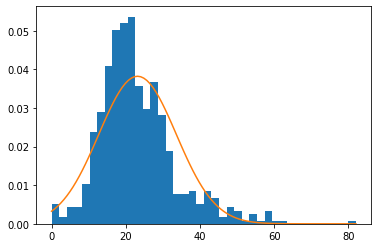
Given this table, we get already a good hihg-level idea of how everything is distributed. However, we want to have a closer look at our target variable steak. So next, we plot the demand distribution by using the histplot function from seaborn - a Python data visualization library.

sns.histplot(df['steak'], bins=40)
plt.show()

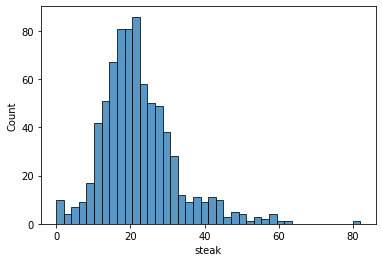
We see that the distribution of steak is right skewed with some outliers above 80. In general, however, it looks like demand follows a normal distribution. In the later part of this tutorial, we will see how we can use this information to solve the newsvendor problem.

Now that we now how our data is distributed, we want to look for pattens in it. We therefore calculate the pairwise correlations between the indiviual columns by using the corr method from pandas.

df.corr()

	is_holiday	is_closed	weekend	wind	clouds	rain	sunshine	temperature	steak
is_holiday	1.000000	0.258811	-0.052268	-0.037678	0.007091	0.080079	-0.019365	-0.046112	-0.116990
is_closed	0.258811	1.000000	0.019884	0.018275	0.004366	0.019916	-0.058785	-0.096162	-0.179780
weekend	-0.052268	0.019884	1.000000	0.007750	0.042130	0.024998	0.003346	-0.015134	0.198166
wind	-0.037678	0.018275	0.007750	1.000000	0.118402	0.051298	-0.061206	-0.019079	0.044674
clouds	0.007091	0.004366	0.042130	0.118402	1.000000	0.195566	-0.862637	-0.340417	0.079553
rain	0.080079	0.019916	0.024998	0.051298	0.195566	1.000000	-0.224358	-0.023531	-0.018303
sunshine	-0.019365	-0.058785	0.003346	-0.061206	-0.862637	-0.224358	1.000000	0.577168	-0.156304
temperature	-0.046112	-0.096162	-0.015134	-0.019079	-0.340417	-0.023531	0.577168	1.000000	-0.158412
steak	-0.116990	-0.179780	0.198166	0.044674	0.079553	-0.018303	-0.156304	-0.158412	1.000000

Instead of straining our eyes to look at the preceding table, it’s nicer to visualize it with a heatmap. This can be done easily with seaborn

# set figure size
plt.figure(figsize=(10, 8))
# plot heatmap
sns.heatmap(df.corr(), vmax=1, vmin=-1, annot=True, linewidths=0.1, cmap='viridis');

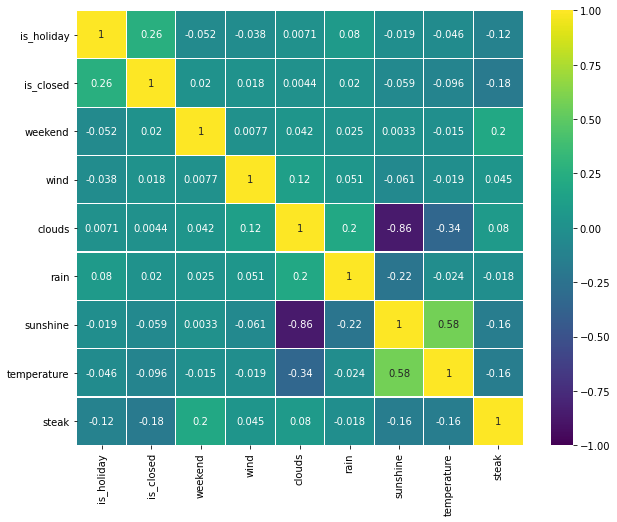
When looking at the table/heatmap, there are two things we are interested in. First, how the individual features are correlated to each other, and second, how the features are correlated to the target variable. With this respect, we note that there is a strong correlation between sunshine and clouds, a medium correlation between sunshine and temperature, and slight correlations between some other weather features (e.g. clouds and temperature). However, these insights are not very surprising, as we are quite familiar with the interdependencies of weather factors. In contrast, we don’t have a clear picture of how weather affects the demand for steak. Looking at the heat map, we see that there seems to be a small correlation with the weather features temperature or sunshine. Moreover, we note that the demand for steak slightly correlates with the features is_closed and weekend.

As you may have already noticed, the calendar features weekday, month, and year are missing in the correlaction matrix above. This is due to the fact, that these are categorical feauters for which we can not compute a correlation. Instead, however, we can use a boxplot to see if there is a relationship between them and the demand for steak. For plotting we use the boxplot function from seabron.

ax = sns.boxplot(x='weekday', y='steak', data=df)

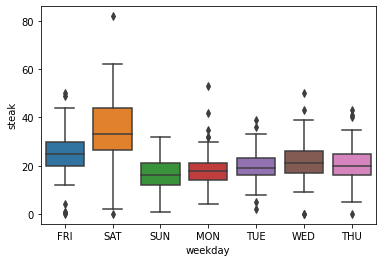
We can clearly observe, that the demand of steak strongly depends on the day of the week. While the highest amount of steak is sold on Saturdays and Fridays, the least amount is sold on Sundays and Mondays. From this information, we can also infer that the binary feature weekend is somewhat problematic, as it summarizes the day with the highest and lowest average demand for steak.

ax = sns.boxplot(x='month', y='steak', data=df)

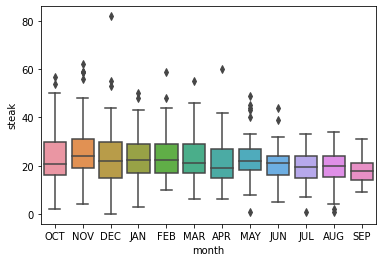
Looking at the month, we see that demand for steak tends to be highest in November and then continuously decreases until September before increasing again in October. This observation is consistent with the slightly negative correlation between “temperature” and “steak,” as steak demand tends to be higher in colder months than in warmer ones.

ax = sns.boxplot(x='year', y='steak', data=df)

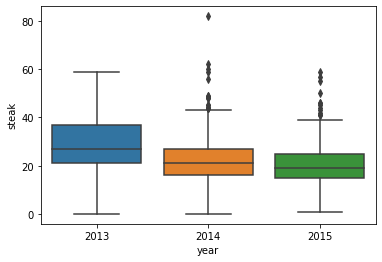
Finally, if we look at the year, we can see that demand is apparently decreasing from year to year.

Data Pre-processing

Up to this point, we have developed a good understanding of the data collected by the restaurant manager. Still, before we can build a model for decision making, we have to do some data pre-processing as the quality of data and the useful information that can be derived from it directly affects the ability of a model to learn.

As a first step it is good practice to check for missing values in the data, which Pandas automatically sets as NaN values. These can be identified by running df.isnull(), which returns a Boolean DataFrame of the same shape as df. To get the number of NaN’s per column, we can use the sum function

df.isnull().sum()

weekday        0
month          0
year           0
is_holiday     0
is_closed      0
weekend        0
wind           0
clouds         0
rain           0
sunshine       0
temperature    0
steak          0
dtype: int64

We see there are no NaN’s, which means we have no immediate work to do in cleaning the data.

As noted before, the Yaz dataset has three categorical variables, weekday, month, and year. However, the models that we are going to use in the cours of this tutorial are based on mathematical equations and thus cannot process text. Therefore, we need to encode the categorical data, i.e., transform it into a numerical representation. One way to do this is to apply one-hot encoding, where each category is converted into a binary column with the values “1” and “0” to indicate whether or not an observation belongs to the respective category. For one-hot encoding, we use the get_dummies method from pandas.

X = pd.get_dummies(X, columns=["weekday","month","year"])
X

	is_holiday	is_closed	weekend	wind	clouds	rain	sunshine	temperature	weekday_FRI	weekday_MON	weekday_SAT	weekday_SUN	weekday_THU	weekday_TUE	weekday_WED	month_APR	month_AUG	month_DEC	month_FEB	month_JAN	month_JUL	month_JUN	month_MAR	month_MAY	month_NOV	month_OCT	month_SEP	year_2013	year_2014	year_2015
0	0	0	0	1.9	7.7	0.1	150	15.9	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	0
1	0	0	1	2.7	6.9	10.7	0	13.2	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	0
2	0	0	1	1.4	8.0	0.4	0	10.6	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	0
3	0	0	0	2.3	6.4	0.0	176	13.3	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	0
4	0	0	0	1.7	8.0	0.0	0	13.5	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
760	0	0	0	1.6	8.0	0.0	0	3.5	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1
761	0	0	0	1.8	2.2	0.0	362	14.6	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1
762	0	0	0	1.8	0.7	0.0	405	14.7	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1
763	0	0	0	1.9	6.9	0.0	44	16.0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1
764	0	0	1	1.9	5.6	0.0	46	17.3	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1

765 rows × 30 columns

Next, we divide the data into a training set containing 75% of the data and a test set containing the remaining 25%. While we use the training set to build a model, we need the test set to evaluate it on unknown data.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, shuffle=False)

As we have already seen at the beginning, the various features in our data vary greatly in magnitudes, units, and range. However, some machine learning algorithms are sensitive to theses different scales. Therefore, we need to transform the independent features in the data to a fixed range. This is what is knowen as feature scaling. Feature scaling can greatly affect the performance of a model and is therefore an essential tasks in pre-processing. Note that there are many different methods for scaling out there. However, which one works best strongly depends on the specific scenario. One of the most common techniques, and the one we will use in the following, is called standardization. Here the data for each feature is transformed to have zero mean and a variance of 1. We can apply Standardization by useing the StandardScaler from sklearn. We first intanziate the scaler and fit it on the training data such that we do not leak any data of our test set. Finally, we transform both, train and test

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

Part 3: Parametric Approach

Now that we are done with preprocessing, we can use our data to determine the optimal inventory quantity of steak.

One way we can use the data is to estimate the true demand distribution based on the past demand samples. As we know from the exploratory data analysis before, the demand for steak seems to follow a normal distribution. We therefore estimate mean \(\mu\) and standard deviation \(\sigma\) to fit a normal distribution to the training data

# determine mean and std
mean = round(y_train.mean(),2)
std = round(y_train.std(),2)
print("Mean:", mean)
print("Std:", std)

Mean: 23.17
Std: 10.44

from scipy.stats import norm

# create normal distribution
normal = norm(mean,std)
normal_x = np.linspace(y_train.min(), y_train.max(), 100)
normal_y = normal.pdf(normal_x)

# plot demand and fitted normal distibution
plt.hist(y_train, bins = 40, density=True)
plt.plot(normal_x, normal_y)
plt.show

<function matplotlib.pyplot.show>

In the next step, we can use this distribution to determine how many steaks to defrost overnight. But before, we have to define the under and overage costs for steak. The store manager tells us that each unit of unsold steak costs 5€ and each unit of demand that cannot be met costs 15€.

cu = 15
co = 5

Finally, we can implement equation (2), which then tells us how many steaks to defrost for a single day (the optimal inventory quantity \(q\)).

# determine optimal inventory quantity
q = norm(mean,std).ppf(cu/(cu+co))
round(q)

30

We call this the traditional parametric approach, we first assume the demand falls in a family of parametric distributions, estimate its parameters based on past demand samples, and then solve the initial optimization problem (2).

To see how well this approach works, we can calculate the average cost associated with our decision for all samples in the training set. For this, we can use the average_costs function available in the ddop.metrics module. The function takes four arguments: the true values, the predicted values, the underage costs, and the overage costs.

# create array with length equal to number of observations in test set filled with the value of the inventory quantity q
y_pred = np.full(y_test.shape[0],q)

from ddop.metrics import average_costs
# calculate average costs
average_costs(y_true=y_test, y_pred=y_pred, cu=cu, co=co)

66.0260614334805

As you can see, we have average costs of 66.02€ associated with our decision. But can we do better? To answer this, let us go back to our data. So far we only used past steak demand samples. However, we have access to exogenous features that may have predictive power for demand. For example, we know from our EDA that the day of the week has an impact on the demand. One way we can take this information into account is to fit a normal distribution for the samples of each weekday, respectively. To do this, we determine mean and standard deviation for each weekday.

days = ['MON','TUE','WED','THU','FRI','SAT','SUN']
mean_std_by_day = pd.DataFrame(columns=("Mean", "Std"), index=days)

for day in days:
  index_list = X_train[X_train["weekday_" + day] == 1].index
  demand = y_train.iloc[index_list]
  mean = round(demand.mean(), 2)
  std = round(demand.std(), 2)
  mean_std_by_day.loc[day] = [mean, std]

mean_std_by_day

	Mean	Std
MON	18.79	7.44
TUE	20.27	6.33
WED	21.26	7.3
THU	21.69	7.18
FRI	26.1	8.57
SAT	37.35	12.83
SUN	16.55	6.08

As before, we can then use these distributions to determine the optimal inventory quantity for each day by solving equation (2).

# determine decision q depending on the weekday
q_by_day = {}
for day in days:
  mean = mean_std_by_day.loc[day]['Mean']
  std = mean_std_by_day.loc[day]['Std']
  q_by_day[day] = round(norm(mean, std).ppf(cu/(cu+co)))
q_by_day

{'FRI': 32, 'MON': 24, 'SAT': 46, 'SUN': 21, 'THU': 27, 'TUE': 25, 'WED': 26}

Given the optimal decision for each weekday, we can write a simple predict function.

def predict(X):
  """
  Get the decision for each sample in X depending on the weekday.

  Parameters
  ----------
  X : Pandas DataFrame of shape (n_samples, n_features)
      The input samples.

  Returns
  ----------
  y : array of shape (n_samples,)
      The predicted values.
  """

  pred = []
  for index, sample in X.iterrows():
    for day in days:
      if sample["weekday_"+day]:
        pred.append(q_by_day[day])

  return np.array(pred)

We apply the function to the test set and calculate the average costs.

# predict optimal inventory quantity
y_pred = predict(X_test)

# calculate average costs
average_costs(y_test, y_pred, cu, co)

54.53125

Now look, we were able to reduce the average costs from 66.02€ to 54.53€. That is a great improvement! But maybe we can do even better by considering the other features of the dataset as well. To do this, we could group observations with same feature values and then estimate a normal distribution for each group - like we did before but now with more features than just the weekday. However, this has two main drawbacks: 1. Imagine we have two features, the weekday and the month. If we were to estimate a distribution for each feature combination, we would have to fit a total of 7*12=84 distributions. That sounds like a lot of work, doesn’t it? 2. To stay with the example: Consider the case where it is Monday and January. As you can see below, we only have 8 samples with the same feature values. Such a small number of samples makes it hard to fit a distribution. Moreover, with an increasing number of features we may not have a single sample with the same feature values.

X_train[(X_train['weekday_MON']==1)&(X_train['month_JAN']==1)].shape[0]

8

Instead of estimating a distribution for each group of samples with the same feature values, we can train a machine learning model to predict the demand. For example, we can use Linear Regression from sklearn.

# predict demand using Linear Regression
from sklearn.linear_model import LinearRegression
LR = LinearRegression()
LR.fit(X_train,y_train)
pred = LR.predict(X_test)

Of course we cannot assume the model to be perfect: first, because of the model error itself, and second, because of the uncertainty in demand. For this reason, we need to adjust the predictions for uncertainty to obtain optimal decisions. We can get a representation of the remaining uncertainty by estimating the distribution of the prediction error on the training set. Assuming the error to be normally distributed, we determine the parameters \(\mu_{e}\) and \(\sigma_{e}\).

# determine mean and standard deviation of the prediction error
error = y_train-LR.predict(X_train)
error_mean = error.mean()
error_std = error.std()

Next, we pass the error distribution to equation (2) to determine an additional safety buffer that adjusts the predictions based on the forecast error by balancing the expected overage and underage costs.

# determine safety buffer
safety_buffer = norm(error_mean, error_std).ppf(cu/(cu+co))

The final order decision is then the sum of both the prediction generated by our model and the safety buffer. More formally, the solution to the newsvendor problem can then be stated as:

\begin{equation} q(x)^{*} = \mu(x)+\Phi^{-1}(\alpha), \tag{3} \end{equation}

where \(\mu(\cdot)\) is the function of the machine-learning model that predicts the demand given feature vector \(x\), and \(\Phi^{-1}\) is the inverse cdf of the error distribution with parameter \(\mu_{e}\) and \(\sigma_{e}\). Consequently, in the next step, we add the safety buffer to the predictions to obtain optimal inventory quantities.

# add safety buffer to the predictions of the model
pred = pred + safety_buffer

Finally, we calculate the corresponding average costs.

# calculate average costs
average_costs(y_test, pred, cu, co)

46.45518848929698

Again, we were able to reduce our average costs from 54.08€ to 46.45€.

Summary

Let us now summarize what we have learned so far:

• In case we do not know the demand distribution, we can estimate the distribution based on past demand samples and then solve equation (2) to determine the optimal inventory quantity.

• We can improve the decision by taking features into account. To do this, we group the data based on their feature values and estimate a distribution for each group. However, this does not work well for a large number of features.

• Instead, we can use a machine-learning model to predict demand. Since we cannot assume the model to be perfect, we estimate the distribution of the prediction error to calculate an additional safety buffer. The optimal decision is then the sum of prediction and safety buffer.

Part 4: Data-Driven Approaches

So far we have only considered the traditional parametric way to solve the newsvendor problem. In this part of the tutorial, we introduce different “data-driven” approaches to solve the newsvendor problem. In contrast to the traditional way of first estimating the demand distribution and then solving the initial optimization problem, these approaches directly prescribe decisions from data without having to make assumptions about the underlying distribution.

Sample Average Approximation

The simplest data-driven approach to solve the newsvendor problem is called Sample Average Approximation (SAA). The idea behind SAA is to determine the optimal inventory quantity by finding the decision \(q\) that minimizes the average cost on past demand samples. Formally, the optimization problem can be stated as follows:

\begin{equation}q^{*}=\min _{q \geq 0} \frac{1}{n} \sum_{i=1}^{n}\left[c u\left(d_{i}-q\right)^{+}+c o\left(q-d_{i}\right)^{+}\right] \tag{4} \end{equation}

where \(n\) is the total number of samples and \(d_i\) is the i-th demand observation. Moreover, \((\cdot)^+\) is a function that returns \(0\) if its argument is negative, and else its argument. Using this function we ensure that we multiply missing units by the underage costs and excess units by the overage costs. To fully understand how SAA works, we go through a simple example.

Example: Determine how many steaks to defrost by applying SAA. The past demand for steak is given by: \(D=[27,29,30]\). You can sell steak in your restaurant for 15€ (underage costs), while unsold units incur overage costs of 5€.

In the following, we try to minimize the optimization problem (4). For simplicity, we do not write down both terms \(cu(d_i-q)^+\) and \(co(q-d_i)^+\). One of them is always zero because we can have either underage units or overage units.

\begin{equation} .....\\ q=27: \frac{1}{3}\Bigl[15*(27-27)+15*(29-27)+15*(30-27)\Bigl]=25\\ q=28: \frac{1}{3}\Bigl[5*(28-27)+15*(29-28)+15*(30-28)\Bigl]=16,67\\ q=29: \frac{1}{3}\Bigl[5*(29-27)+15*(29-29)+15*(30-29)\Bigl]=8,33\\ q=30: \frac{1}{3}\Bigl[5*(30-27)+5*(30-29)+15*(30-30)\Bigl]=6,67\\ q=31: \frac{1}{3}\Bigl[5*(31-27)+5*(31-29)+5*(31-30)\Bigl]=11,67\\ ..... \end{equation}

Based on our calculation, the optimal decision is given by \(q=30\).

Now that we know how SAA works, we can apply the approach on the Yaz dataset by using the class SampleAverageApproximationNewsvendor from the ddop.newsvendor module. To initialize the model we pass the under and overage costs to the constructor. Subsequently, we fit the model to the past demand samples and determine the optimal decision using the predict method.

from ddop.newsvendor import SampleAverageApproximationNewsvendor
SAA = SampleAverageApproximationNewsvendor(cu,co)
SAA.fit(y_train)
SAA.predict()

array([[28]])

Based on SAA the optimal decision is 28. To get a representation of the model performance, we use the score function, which computes the negated average cost. In contrast to the average_costs function this has the advantage that we can calculate the costs directly without having to predict all training examples first.

-SAA.score(y_test)

59.947916666666664

With average cost of 59.95€, SAA performs better compared to the traditional parametric approach without features (66.46€). In contrast, SAA performs worse compared to the parametric approach with features (46.45€). However, this is not really surprising since we already know that exogenous features can improve decision making.

Weighted Sample Average Approximation

Even though SAA is a common and effective approach, it only considers past demand samples. However, in the first part of the tutorial we have seen that we can improve our decision by taking into account features such as the weekday. We now want to do the same here by determining the optimal SAA decision for each weekday separately.

# determine q depending on the weekday using SAA
q_by_day = {}

SAA = SampleAverageApproximationNewsvendor(cu,co)

for day in days:
  index_list = X_train[X_train["weekday_" + day] == 1].index
  demand = y_train.iloc[index_list]
  SAA.fit(demand)
  q_by_day[day] = SAA.predict().item(0)

print(q_by_day)

{'MON': 21, 'TUE': 24, 'WED': 26, 'THU': 26, 'FRI': 31, 'SAT': 45, 'SUN': 20}

Given the optimal decision for each day, we can write a new prediction function.

def predict(X):
  """
  Get the prediction for each sample in X depending on the weekday.

  Parameters
  ----------
  X : Pandas DataFrame of shape (n_samples, n_features)
      The input samples.

  Returns
  ----------
  y : array of shape (n_samples,)
      The predicted values.
  """

  pred = []
  for index, sample in X.iterrows():
    for day in days:
      if sample["weekday_"+day]:
        pred.append(q_by_day[day])

  return np.array(pred)

We can then apply the function on the test set and calculate the average costs:

pred = predict(X_test)
average_costs(y_test,pred,cu,co)

52.057291666666664

Again, we were able to reduce the average costs from 60.24€ to 52.06€ by taking into account the weekday. We can now go a step further by considering more features. To do this, we could use a separate model for the samples with the same feature values. However, as we have seen in the traditional parametric approach, this can become problematic when we have only a small number of samples with the same feature values. Another way to take feature information into account is to determine a weight for each sample based on the similarity to a new instance and optimize SAA against a re-weighting of the data. To determine the sample weights, we can use different machine learning techniques, such as a regression tree. For a better understanding, consider the following example.

Example: Say we have the following past demand samples with feature vector \(x_i=(Weekend, Temperature)\) and we want to calculate their weights based on a new sample \(x=(0,18)\).

Sample	Weekend	Temperature [in °C]	Demand
1	0	19	27
2	1	25	29
3	1	23	30
4	0	25	18
5	0	24	20
6	0	22	23
7	0	11	21

First, we train a regression tree to predict the demand given the features weekend and temperature. The resulting tree looks like this:

The regression tree splits our data into four leafs based on the two features. To determine the sample weights, we look to which leaf the new instance \(x=(0,18)\) belongs. In the first level of the tree we follow the left path since it is no weekend. Then, given the temperature forecast of \(18°C\), we end up in leaf 1 together with sample 1, 6, 7. This means that these observations are most similar to \(x\). Using this information, we assign a weight of \(\frac{1}{3}\) to each of the three samples falling into the same leaf. The sample weights are then given by:

\begin{equation} w_1=\frac{1}{3},\:w_2=0,\:w_3=0,\:w_4=0,\:w_5=0,\:w_6=\frac{1}{3},\:w_7=\frac{1}{3} \end{equation}

Now that we have calculated the sample weights, we can solve the optimization problem like before. The only difference is that we multiply each observation with its corresponding weight, which indicates the similarity to the new sample.

\begin{equation} q=18: \frac{1}{3}\bigl[15*(27-18)\bigl]+...+\frac{1}{3}\bigl[15*(23-18)\bigl]+\frac{1}{3}\bigl[15*(21-18)\bigl] = 85\\ ......\\ q=26: \frac{1}{3}\bigl[15*(27-26)\bigl]+...+\frac{1}{3}\bigl[5*(26-23)\bigl]+\frac{1}{3}\bigl[5*(26-21)\bigl] = 18.33\\ q=27: \frac{1}{3}\bigl[15*(27-27)\bigl]+...+\frac{1}{3}\bigl[5*(27-23)\bigl]+\frac{1}{3}\bigl[5*(27-21)\bigl] = 16.67\\ q=28: \frac{1}{3}\bigl[5*(28-27)\bigl]+...+\frac{1}{3}\bigl[5*(28-23)\bigl]+\frac{1}{3}\bigl[5*(28-21)\bigl] = 21.67\\ ......\\ q=30: \frac{1}{3}\bigl[5*(30-27)\bigl]+...+\frac{1}{3}\bigl[5*(30-23)\bigl]+\frac{1}{3}\bigl[5*(30-21)\bigl] = 30.67 \end{equation}

Based on our calculation, \(q=27\) is the quantity minimizing the average costs on the weighted samples.

We call this approach “weigthed Sample Average Approximation (wSAA)” as it can be seen as weighted form of SAA. More formally the problem can be stated as follows:

\begin{equation} q(x)^*=\min_{q\geq 0} \sum_{i=1}^{n}w_i(x)\bigl[cu(d_i-q)^+ + co(q-d_i)\bigl], \tag{5} \end{equation}

where \(x\) is the feature vector of a new instance and \(w_i(\cdot)\) is a function that assigns a weight \(w_i\in [0,1]\) to each past demand sample \(d_i\) based on the similarity of \(x_i\) and \(x\). In the example above we used a weight function based on a decision tree (DT), given by:

\begin{equation} w_{i}^{Tree}(x)=\frac{\mathbb{1}[x_i \in R(x)]}{N(x)}, \end{equation}

where \(\mathbb{1}\) is the indicator function, \(R(x)\) is the leaf containing \(x\), and \(N(x)\) is the number of samples falling into leaf \(R(x)\). In other words, the function will give a weight of \(\frac{1}{N(x)}\) to sample \(i\) if \(x_i\) belongs to the same leaf as the new instance \(x\), and otherwise zero.

Instead of using a DT, we can also use other machine learning methods to determine the sample weights, for example k-nearest-neighbors (kNN):

\begin{equation} w_{i}^{k \mathrm{NN}}(x)=\frac{1}{k} \mathbb{1}\left[x_i \text { is a } k \mathrm{NN} \text { of } x\right], \end{equation}

where \(k\) is the number of neighbors. In simple terms, the function will give a weight of \(\frac{1}{k}\) to sample \(x_i\) if it is a k-nearest-neighbor of \(x\).

We can apply these approaches on our dataset by using the class DecisionTreeWeightedNewsvendor andKNeighborsWeightedNewsvendor from the ddop.newsvendor module. To initialize the models, we pass the overage- and underage costs to the constructor. Moreover, we define some addition model-specific parameters. For instance, we set the maximum depth for DecisionTreeWeightedNewsvendor to \(6\) and the number of neighbors for KNeighborsWeightedNewsvendor to \(37\). After we have initialized our models we fit them on the training data and calculate the average costs on the test set by using the score function:

from ddop.newsvendor import DecisionTreeWeightedNewsvendor, KNeighborsWeightedNewsvendor
DTW = DecisionTreeWeightedNewsvendor(cu=cu, co=co, max_depth=6,random_state=1)
DTW.fit(X_train, y_train)
DTW_score = DTW.score(X_test,y_test)
print("Avg. cost DTW: ",-DTW_score)

kNNW = KNeighborsWeightedNewsvendor(cu=cu, co=co, n_neighbors=37)
kNNW.fit(X_train_scaled, y_train)
kNNW_score = kNNW.score(X_test_scaled,y_test)
print("Avg. cost kNNW: ", -kNNW_score)

Avg. cost DTW:  46.744791666666664
Avg. cost kNNW:  46.276041666666664

As we can see from our results, the WSAA approach based on kNN outperforms all other models we have seen so far.

---

Empirical Risk Minimization

With wSAA we already got to know a data-driven approach that is able take exogenous features into account. However, to obtain a decision \(q\), we have to first determine weights and then solve an optimization problem for every new sample \(x\). But wouldn’t it be great to learn a function that instead maps directly from features \(x\in X\) to a decision \(q\in Q\)? A natural way to obtain such a function is through empirical risk minimization: \begin{equation} \min_{q(\cdot)\in\mathcal{F}} \frac{1}{n}\sum_{i=1}^{n}\bigl[cu(d_i-q(x_i))^+ + co(q(x_i)-d_i)^+\bigl], \tag{6} \end{equation}

where: - \(x_i\) is the feature vector of the i-th sample - \(d_i\) is the corresponding demand value - \(q(\cdot)\) is the function that maps from feature space \(X\) to decision space \(Q\) - \(\mathcal{F}\) is the function class of \(q(\cdot)\)

In simple terms, we try to find the function \(q(\cdot):X\rightarrow Q\) that minimizes the average costs on our \(n\) past demand samples (the empirical risk). The most straightforward way to do this is based on linear regression.

Linear Regression

Let us consider the following example to see how we can find the function \(q(\cdot)\) that minimizes the empirical risk.

Example: Suppose we have only a single feature, say temperature, and given the value for the temperature we want to know how many steaks to defrost. In other words, we want to find a function \(q(x)\) that maps from temperature \(x\) to a decision \(q\). Of course, the first thing we need to do is to collect some data.

Sample	Temperature [in °C]	Demand
1	5	16
2	7	12
3	10	14
4	12	10
5	15	11
6	18	7
7	20	9
8	21	6
9	23	8
10	25	4

We plot the data and it looks like there is a linear relationship between temperature and demand (see figure below). Consequently, to solve our problem the first thing that comes into mind is linear regression. For this reason, we construct a linear function \(q(x)=b+w*x\), where \(b\) is the intercept term, and \(w\) is a weight. We can think of the intercept as a base demand to which we add or subtract a certain amount depending on the temperature \(x\) and weight \(w\). To find the optimal mapping from temperature to demand, we now have to learn the best fitting values for \(b\) and \(w\). We start by setting \(b=16\) and \(w=-0,4\), which gives us function \(q(x)=16-0,4*x\) that already fits the data quite well. Still, for each sample \(i\) we obtain an error representing the difference between the actual demand \(d_i\) and the estimated decision of \(q(x_i)\). In the figure below these errors are illustrated as dotted lines.

According to linear regression, the goal would be to adjust the values for \(b\) and \(w\) in a way that minimizes the mean difference (error) between the actual demand and the estimated decision. Formally speaking: \begin{equation} \min_{b,w} \frac{1}{n}\sum_{i=1}^{n}\bigl\vert d_i-(b+w*x)\bigl\vert \end{equation}

In our case, however, this can be problematic because overage would have the same effect as underage. Now recall that each unit of unsold steak costs 5€, while each unit of demand that cannot be satisfied costs 15€. In other words, one unit too little costs three times more than one unit too much. Consequently, we try to minimize the average cost rather than the mean difference. The resulting optimization problem is then given by:

\begin{equation} \min_{b,w} \frac{1}{n}\sum_{i=1}^{n}\bigl[cu(d_i-q(b+w*x_i))^+ + co(q(b+w*x_i)-d_i)^+\bigl] \end{equation}

Doesn’t this look like equation \((6)\), which we introduced at the very beginning of this chapter? The only difference is that we have defined \(q(\cdot)\) as a linear decision function of the form \(q(temp)=b+w*temp\). To solve this optimization problem, we can use the class LinearRegressionNewsvendor from ddop.newsvendor.

from ddop.newsvendor import LinearRegressionNewsvendor

temp = [[5],[7],[10],[12],[15],[18],[20],[21],[23],[25]]
demand = [16,12,14,10,11,7,9,6,8,4]
mdl = LinearRegressionNewsvendor(cu=15,co=5)
mdl.fit(X=temp,y=demand)

LinearRegressionNewsvendor(co=5, cu=15)

After fitting the model, we can access the intercept term \(b\) via the argument intercept_ and the weight \(w\) via the argument feature_weights_.

print("b:",mdl.intercept_)
print("w:",mdl.feature_weights_)

b: [18.333333]
w: [[-0.46666667]]

Thus, the function \(q(\cdot)\) that fits our data best is given by:

\begin{equation} q(temp)=18.3-0.47*temp \end{equation}

In the next step we want to know how many steaks to defrost for tomorrow. We check the weather forecast, which tells us that it will be 25 degrees. Given the temperature, the function \(q(\cdot)\) then tells us that the optimal inventory stock is: \(18.3-0.47*10=13.6\). Instead of determining the decision ourselves, we can also use the model’s ´predict` method:

mdl.predict([[10]])

array([[13.6666663]])

Of course, this was just a simple example to illustrate the concept of this approach. As we know, the Yaz dataset provides a lot more features than just the temperature. Consequently, we are looking for a function of the form:

\begin{equation} q(x)=b+w_1*x_1+...+w_m*x_m=b+\sum_{j=1}^{m}w_j*x_j, \tag{7} \end{equation}

where \(x_j\) represents the value of feature \(j\)-th from sample \(x\), and \(w_j\) is the corresponding feature weight. As a result, the optimization problem that we want to solve becomes:

\begin{equation} \min_{b,w_1,..,w_m} \frac{1}{n}\sum_{i=1}^{n}\bigl[cu(d_i-b-\sum_{j=1}^{m}w_j*x_{i,j})^+ + co(b+\sum_{j=1}^{m}w_j*x_{i,j}-d_i)^+\bigl], \tag{8} \end{equation}

We now have to learn the value for intercept term \(b\) and feature weights \(w_1,...,w_m\). For now, we do this just for the temperature and the weekdays. Note that we use the one hot encoded version of the data, thus each weekday is represented by a binary column.

cols = ['temperature', 'weekday_MON', 'weekday_TUE', 'weekday_WED', 'weekday_THU', 'weekday_FRI', 'weekday_SAT', 'weekday_SUN']
LRN = LinearRegressionNewsvendor(cu=15,co=5)
LRN.fit(X_train[cols],y_train)
print(LRN.intercept_)
print(LRN.feature_weights_)

[23.268817]
[[-0.21505376  1.5913978   3.8494624   5.3225806   4.4946237   9.9892473
  23.817204    0.        ]]

We note that the intercept term is 23.27. This is now our base demand to which we add or subtract a certain amount, depending on corresponding feature values. For example, we add 23.82 for a Saturday. In contrast, we subtract 1.59 for a Monday. The weight for the temperature is -0.215 so we would subtract 2.15 in case it is 10°C. At this point it should be clear how this approach works and how the parameters are to be interpreted. So in the next step, we can apply the model to our dataset.

LRN = LinearRegressionNewsvendor(cu=15,co=5)
LRN.fit(X_train,y_train)
-LRN.score(X_test,y_test)

49.281382612348956

With average costs of €49.28 the model performs slightly worse compared to the wSAA approaches. However, it outperforms most other approaches we have considered so far.

Deep Learning

In the previous section, we assumed that the demand is a linear combination of features. To find the perfect mapping from features \(x\) to decision \(q\) we therefore specified that \(q(\cdot)\) belongs to the class of linear decision functions. However, sometimes there is no linear relationship, so we need a nonlinear function to describe our data. One way to obtain such a function is by using a deep neural network (DNN).

A DNN uses a cascade of many layers to obtain an output given some input data. In general, it can be distinguished between input-, hidden-, and output-layer, each consisting of a number of neurons. In the first layer the number of neurons corresponds to the number of inputs. In other words, each neuron takes the value of a single feature as input, e.g. the temperature or the weekday. The input-layer is followed by a number of hidden-layers, each presented by an arbitrary number of neurons. In the output-layer the number of neurons corresponds to the number of outputs. In our example, we only have a single neuron that outputs the decision \(q\) conditional on the features temperature and weekday. The individual neurons of a layer are each connected to the neurons of the layer before and behind. In a graph, the neurons can be represented as nodes and their connections as weighted edges. A neuron takes the outputs of the neurons from the previous layer as inputs. Subsequently, it computes the weighted sum of its inputs and adds a bias to it. Formally speaking:

\begin{equation} bias+\sum_{l=1}^{L}x_l*w_l, \tag{9} \end{equation}

where \(x_l\) is the \(l\)-th input of a neuron and \(w_l\) the corresponding weight. Does this look familiar? This is the exactly the decision function \((7)\) that we used in the regression based approach before. The only difference is that we use the term “bias” for the constant value instead of “intercept”. But what does this mean? If we were just to combine a set of linear functions, we would get a single linear function as a result. In other words, there would be no difference to the previous approach. This is where the activation function comes into play. The activation function is a non-linear function that transforms the computed value of equation (9) and then outputs the final result of a neuron. For example, the Rectified Linear Unit (ReLU) activation function outputs \(0\) if the input value is negative and its input otherwise. Thus, the DNN models a piecewise linear function, which may looks like this:

The goal of the network is then to find the function that fits the data best. To find such a function in the linear regression based model, we had to determine the optimal values for the feature weights and the intercept term. This is basically the same here. We just have a lot more weights and intercept terms (biases). Since we are trying to obtain cost-optimal decisions, the network tries to determine the unknown parameters in a way that minimizes the average costs on our data. Thus, the problem can be stated as follows:

\begin{equation} \min_{w,b} \frac{1}{n}\sum_{i=1}^{n}\bigl[cu(d_i-\theta(x_i;w,b))^+ + co(\theta(x_i;w,b)-d_i)^+\bigl], \tag{10} \end{equation}

where \(\theta(\cdot)\) represents the function of the network with weights \(w\) and biases \(b\). Now look, this is again similar to equation \((6)\). The only difference is that \(q(\cdot)\) is represented by a DNN.

To apply this approach on the Yaz dataset we can use the class DeepLearningNewsvendor from ddop.

from ddop.newsvendor import DeepLearningNewsvendor
DLN = DeepLearningNewsvendor(cu=15,co=5)
DLN.fit(X_train_scaled,y_train)
-DLN.score(X_test_scaled,y_test)

49.79702285180489

For this model the average cost are higher compared to both the linear regression based model and the WSAA models. One reason for this might be that a neural network often needs more data to learn a good decision function.

Summary

In this part of the tutorial we have seen three different data-driven approaches to solve the newsvendor problem.

• In the simplest case where we only have past demand observations we can use sample average approximation (SAA) to solve the newsvendor problem. The goal of SAA is to find the decision \(q\) that minimizes the average costs on past demand samples.

• However, we have seen that additional demand features can improve decision making, since they usually reduce the degree of uncertainty.

• With weighted sample average approximation (wSAA) and empirical risk minimization (ERM) we got to know two data-driven approaches that can take such features into account by learning a function \(q(\cdot)\) that maps from features \(x\) to a decision \(q\).

• wSAA, on the one hand, defines the function \(q(\cdot)\) point-wise. It is based on deriving sample weights from features and optimizing SAA against a re-weighting of the training data. To determine the weights we can use different weight functions, e.g., based on KNN or DT regression.

• The ERM approach, on the other hand, tries to find the function \(q(\cdot)\) that maps from features to a decision by minimizing its empirical risk. Therefore, we have to specify the function space to which the decision function belongs. With LinearRegressionNewsvendor, and DeepLearningNewsvendor we have seen two models that define \(q(\cdot)\) in a different manner. While the former one assumes that \(q(\cdot)\) is a linear decision function, the latter one defines \(q(\cdot)\) as non-linear function by using as a deep neural network.

A Final Note

In this tutorial, you learned how to solve the newsvendor problem based on past demand data. For the specific case of Yaz and the data for the product “steak”, you have seen that several data-driven algorithms can outperform the traditional parametric approach. The best method has been shown to be wSAA with a weight function based on k-nearest-neighbors regression. However, it is important to note that there is no such thing as “the best model”. Which model performs best can vary from one task to another. It may depend on the cost parameters, the number of features or the size of the dataset. This is exactly the reason why ddop provides easy access to a set of different models that can be used to find the best one for a given problem. As a next step, you can now build up on what you have learned and apply the different algorithms to some other data. For example, you can start by using the data for a product other than “steak”, or even several products at once. Alternatively, you can use the bakery dataset that is also provided within ddop.

So far, we have seen a number of different approaches to solve the newsvendor problem. In the end however, we want to select the best model and use it for decision making. To determine which model is best, we used a part of our data to train a model while we used the remaining part to estimate its performance on unseen data. The problem with this approach is that the performance depends on how we split the data. We can simply demonstrate this by determining the average costs for a model with two different train and test sets (we use the same train size but a different random state).